Understanding percentages is a fundamental math skill that can help you solve various financial problems efficiently. In this blog post, you will learn how to calculate a total sum when given a percentage of it, specifically when 28% of a sum equals $80. By following simple mathematical steps, you’ll gain clarity and boost your confidence in handling similar problems that may arise in your daily life or studies. Let’s probe the process and uncover the sum you’re looking for.
Key Takeaways:
- Understanding percentage: The problem involves finding a total sum based on a percentage value, which is a common mathematical concept.
- Setting up the equation: To find the sum, you can set up the equation: 0.28 * Sum = 80.
- Solving for Sum: Dividing both sides of the equation by 0.28 allows you to isolate and solve for the Sum.
- Calculation: By performing the division, the Sum can be calculated as approximately $285.71.
- Real-world application: This type of calculation is useful in financial situations, such as budgeting or determining discounts.
Understanding Percentages
Before venturing into calculations, it’s necessary to grasp the concept of percentages. Percentages allow you to express a portion of a whole in terms of 100, making it easier to compare and analyze values. By understanding how percentages work, you’re better equipped to make informed decisions in various situations, whether in budgeting, shopping, or assessing data.
Definition of Percentage
The percentage is a number or ratio expressed as a fraction of 100. It represents a part of a whole, allowing you to determine how much one quantity is relative to another. For example, if you have 25 out of 100 apples, you have 25%, or a quarter, of the total number of apples.
How Percentages Relate to Sums
Percentages play a significant role in understanding sums, as they allow you to quantify and compare values. When you know the percentage of a sum, you can easily calculate the total amount. In your case, 28% of a sum equates to a specific dollar amount, which can be used to derive the total sum.
Understanding how percentages relate to sums is crucial for making financial decisions. When you know what percentage represents a certain dollar amount, you can work backwards to find the total sum. This concept applies to various real-life scenarios, such as discounts during shopping or calculating tips at restaurants. Recognizing these relationships empowers you to navigate financial calculations with ease and confidence.
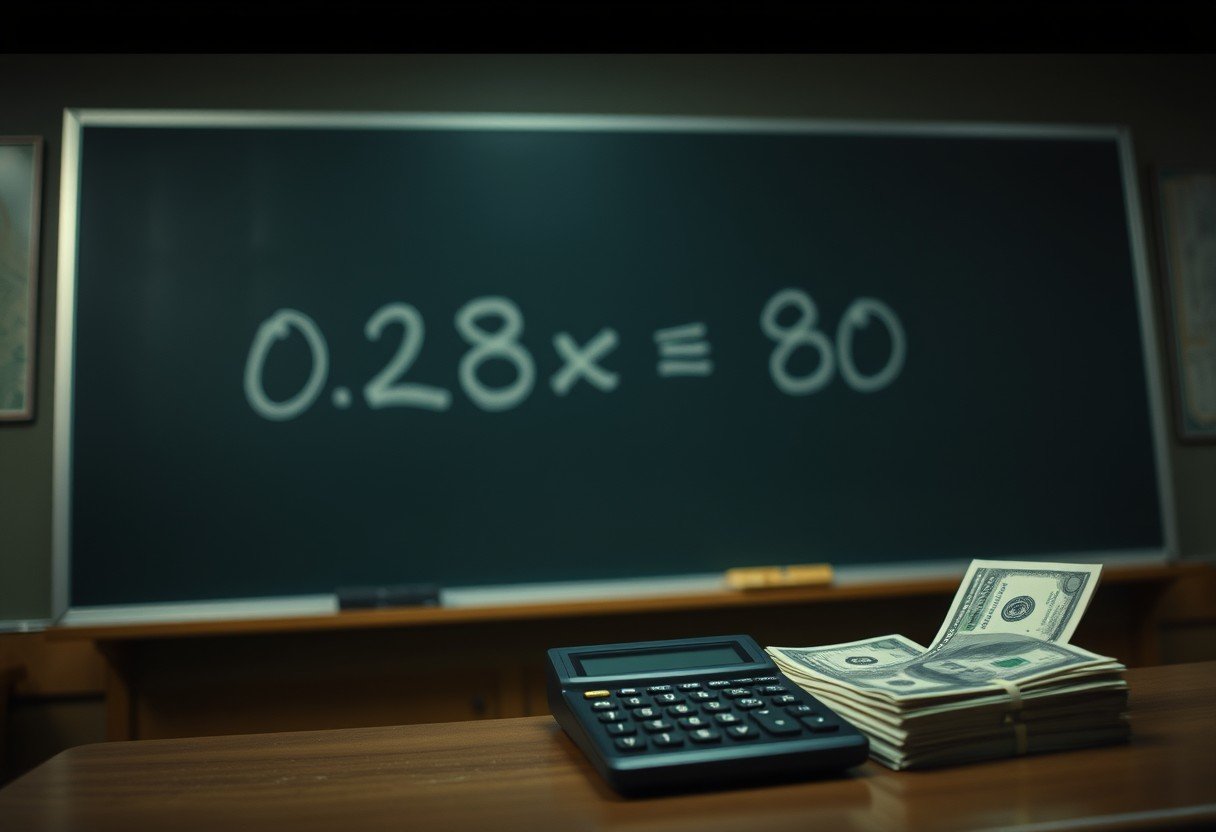
Setting Up the Equation
Even though mathematical problems can seem daunting at first, breaking them down into manageable steps can simplify the process. For the equation we are trying to solve, it’s crucial to understand how to represent the conditions of the problem mathematically. This involves identifying the percentage and the relationship between the part and the whole, leading you to formulate a clear equation that can be solved easily.
Identifying the Given Information
Setting the stage for solving the problem involves carefully identifying the given information. You know that 28% of a sum equals $80. This means you already have two pieces of important data: the percentage (28%) and the result of that percentage of the sum ($80). Keeping these figures in mind will be important as you move forward with solving the equation.
Formulating the Equation
To create the equation that represents the problem, start by expressing the relationship stated in the prompt mathematically. Since 28% of a sum (let’s denote the sum as ‘S’) is equal to $80, you can formulate the equation as 0.28S = 80. This equation clearly ties your given percentage to the unknown sum you are trying to find.
Identifying this equation is key because it provides a direct path to finding the solution. You will use the equation 0.28S = 80 to isolate the variable ‘S’ or the sum. By continuing with algebraic principles, you’ll be able to find the value of ‘S’, allowing you to answer the original question accurately.
Solving for the Sum
Not every mathematical problem has to be daunting. In this case, you need to determine the total sum from a percentage. To find this sum, you’ll simply set up a simple equation based on the information provided. Understanding the relationship between percentages and their corresponding amounts is crucial in solving this problem efficiently.
Steps to Isolate the Variable
On your journey to find the sum, you’ll first need to express the problem as an equation. Since 28% of the unknown sum equals $80, you can write this as 0.28x = 80, where x represents the sum. By isolating the variable x, you can simplify the equation, paving the way to find its value.
Calculation of the Sum
For the final calculation, you will divide both sides of the equation by 0.28. This will enable you to solve for x, which is your unknown sum. After completing this step, you’ll arrive at the value of the total amount you are seeking.
Isolate x by performing the calculation: x = 80 / 0.28. As you do this, you’ll find yourself closer to understanding the problem’s solution. The result will give you the complete sum you need, allowing you to confidently answer the question and carry that knowledge forward into other percentage-related problems.
Verification of the Result
Now that you have calculated the sum, it’s necessary to verify your result to ensure accuracy. Verification involves revisiting your calculations and confirming that the derived sum aligns with the initial conditions of the problem. By doing this, you can gain confidence in your solution and ensure that it accurately reflects the relationship between the percentage and the total sum.
Checking the Calculation
To check your calculation, you simply need to reverse the process you used to find the sum. Multiply your calculated sum by 28% and see if it equals $80. If it does, you can be assured that your computation is correct and aligns with the original problem statement.
Ensuring the Value Makes Sense
Any derived value should not only be mathematically accurate but also practical within the context of the problem. It’s important to consider if the total sum feels reasonable based on the percentage provided and the value it generates. If the number seems outlandish or unrealistic, it’s time to reassess your calculations.
Result-oriented verification is crucial; it helps you grasp the context of your findings. You should reflect on whether the sum you derived is a reasonable total given that 28% results in $80. By evaluating its practical implications, you ensure your final answer is not just correct mathematically but also valid within real-world scenarios. This step builds confidence in your results and demonstrates the importance of critical thinking in problem-solving.
Applications of the Concept
Unlike many mathematical concepts, understanding how to find a sum from a percentage has practical implications in various aspects of your life. From budgeting and shopping to interpreting discounts and financial planning, knowing how to manipulate percentages can lead to better financial decisions. This skill empowers you to navigate everyday situations, making it easier to understand prices, savings, and investment returns.
Real-Life Examples of Percentages
Any time you shop, you encounter percentages—sales, discounts, taxes, and tips all rely on this concept. For example, when a store advertises a 20% discount on an item priced at $100, you can quickly determine how much you save and the final price. These calculations are fundamental to making savvy purchases, ultimately influencing your spending habits.
Importance in Financial Literacy
Literacy in financial concepts, especially percentages, is important for navigating your financial landscape effectively. Whether buying a car, renting an apartment, or investing in the stock market, understanding percentages helps you assess the true value and impact of financial decisions.
Understanding how percentages affect your finances can significantly enhance your ability to make informed choices. By grasping this concept, you can evaluate potential returns on investments, understand mortgage rates, and differentiate between promotional offers. This knowledge not only aids in everyday transactions but also fosters long-term financial growth, empowering you to build a secure future.
Common Mistakes and Misconceptions
Your understanding of percentages can often be clouded by common mistakes. Many individuals assume that percentage calculations are straightforward, leading to misinterpretations of the data. For instance, they might miscalculate the percentage itself or fail to convert it into the correct decimal format before performing operations. Being aware of these pitfalls can significantly improve your accuracy and confidence in handling percentage problems.
Errors in Percentage Calculations
On many occasions, errors in percentage calculations stem from a misunderstanding of the percentage’s underlying principles. Some may inaccurately add or subtract percentages rather than applying the proper formula. Additionally, miscalculating the total amount that the percentage is derived from can lead to wrong conclusions, reinforcing the need for careful computation.
Tips for Accurate Computation
Tips for ensuring accurate computations revolve around understanding and applying effective strategies. Here are a few key points to keep in mind:
- Always convert the percentage to a decimal format before calculations.
- Double-check your arithmetic to avoid simple errors.
- Use a calculator for larger sums to minimize human error.
Recognizing these approaches can enhance your ability to perform percentage calculations with confidence.
For instance, enhancing your skills in accurate computation can significantly impact your understanding of percentages. Consider these additional strategies:
- Break down complex calculations into smaller, manageable steps.
- Review foundational concepts related to fractions and decimals for better percentage awareness.
- Practice with various examples until you’re comfortable with different scenarios.
Recognizing these methods will empower you to tackle percentage problems effectively.
Final Words
Drawing together the concepts explored, you can efficiently determine the sum when 28% equals $80 by applying basic algebra. By setting up the equation 0.28x = 80 and solving for x, you find that the sum is $285.71. Understanding these calculations equips you with valuable skills for handling percentages in real-life financial situations, empowering you to make informed decisions confidently.
FAQ
Q: If 28% of a sum is $80, how do I find the total sum?
A: To find the total sum, you can use the formula for calculating the percentage. If 28% of a sum (let’s call it ‘S’) is equal to $80, you can set up the equation: 0.28 * S = 80. To find S, divide both sides by 0.28, giving you S = 80 / 0.28, which equals approximately $285.71.
Q: What formula should I use to solve problems like this one?
A: The formula you should use is the percentage formula, which is: Percentage = (Part / Total) * 100. Rearranging this formula allows us to find the total given the part and the percentage. For this case, you can also directly use the equation suggested above, where Total = Part / (Percentage/100).
Q: Can this method be applied to other percentage problems?
A: Yes, this method is generally applicable to any problem involving percentages. Whenever you know a part and its corresponding percentage of the whole, you can easily find the total by rearranging the formula as shown. Just remember to convert the percentage into a decimal by dividing by 100.
Q: How can I check if my answer is correct once I find the sum?
A: To check if your answer is correct, you can simply calculate the percentage of the found sum and see if it matches the part you started with. In this case, after finding a total sum of approximately $285.71, you would calculate 28% of it by multiplying 285.71 by 0.28 to see if it equals $80.
Q: What if the percentage value was different, how would that affect the result?
A: If the percentage value was different, the total sum would change accordingly. A higher percentage would result in a lower total sum, whereas a lower percentage would yield a higher total sum. The relationship is inversely proportional; thus, adjusting the percentage will directly affect the total you calculate.








Leave a Comment