Figuring out a total amount when you only know a part of it can seem tricky, but it’s a useful skill for everyday life. Whether you’re calculating a discount, understanding a budget, or just solving a math problem, the process is straightforward. This guide will walk you through exactly how to find the total sum when you know that 28% of it equals $80, giving you the confidence to handle any similar percentage puzzle.
Grasping the Basics of Percentages
Before we solve the problem, let’s quickly review what a percentage is. The word “percent” literally means “per hundred.” So, a percentage is just a special way of showing a fraction of a whole, where the whole is always 100.
For example, 50% means 50 out of 100, which is half. In our problem, 28% means 28 parts out of a total of 100 parts. Understanding this concept is the first step to solving our question.
When dealing with calculations, it’s easiest to convert the percentage into a decimal or a fraction. To turn a percentage into a decimal, you simply divide it by 100. So, 28% becomes 0.28. This conversion is the key to setting up our equation correctly.
Setting up the Correct Equation
Translating a word problem into a mathematical equation makes it much easier to solve. The problem states that “28% of a sum is $80.” We can break this down into a simple formula.
Let’s use the letter ‘S’ to represent the unknown total sum we are trying to find. Using our decimal from the previous step, we can write the equation like this:
0.28 * S = 80
This equation perfectly represents the problem. It reads as “0.28 (which is 28%) of the Sum (S) equals $80.” Now, we have a clear path to finding the value of S.
The Step-by-Step Calculation to Find the Sum
With the equation set up, solving for the total sum ‘S’ involves a simple algebraic step. Our goal is to get ‘S’ by itself on one side of the equation. Since ‘S’ is currently being multiplied by 0.28, we need to do the opposite operation to isolate it.
The opposite of multiplication is division. Therefore, we will divide both sides of the equation by 0.28. This will cancel out the 0.28 on the left side, leaving ‘S’ all by itself.
Here is the process broken down into simple steps:
- Start with your equation: 0.28 * S = 80
- To isolate S, divide both sides by 0.28: (0.28 * S) / 0.28 = 80 / 0.28
- This simplifies the equation to: S = 80 / 0.28
- Perform the division: S = 285.7142…
Since we are dealing with money, we should round the result to two decimal places. Therefore, the total sum is approximately $285.71.
How to Verify Your Answer is Correct
A great habit in math is to always check your work. Verifying your answer ensures accuracy and helps you understand the relationship between the numbers. To check our result, we can simply plug our answer back into the original problem statement.
Does 28% of $285.71 equal $80? Let’s find out.
We multiply our calculated sum by the decimal form of the percentage: $285.71 * 0.28 = $79.9988. This result is extremely close to $80. The tiny difference is only due to our rounding in the previous step. This confirms our calculation is correct.
Real-World Scenarios Where This Math is Useful
You might think this is just a textbook problem, but this type of calculation appears frequently in real life. Knowing how to work backward from a percentage can empower you to make smarter financial decisions.
This skill is essential for understanding your finances and making informed choices daily.
Here are a few examples:
- Shopping and Discounts: If an item is on sale for $80, and you know this was a 28% discount, you can calculate the original price to see the true value of the deal.
- Budgeting: If you know that your $80 weekly food expense represents 28% of your total weekly budget, you can calculate your total budget to see if you are on track with your financial goals.
- Calculating Tips: If you left a $80 tip and want to know what percentage it was of the bill, or vice-versa, this same formula applies.
This fundamental math helps you navigate financial situations with much more confidence.
Avoiding Common Pitfalls in Percentage Problems
Percentage calculations can sometimes be tricky, and a few common mistakes can lead to the wrong answer. Being aware of these potential errors will help you improve your accuracy.
The most frequent error is forgetting to convert the percentage into a decimal before calculating. Multiplying by 28 instead of 0.28 would give a wildly incorrect answer. Another common mistake is applying the percentage to the wrong number, especially in more complex problems involving increases or decreases.
To help you stay on track, here is a quick comparison of correct versus incorrect approaches.
| Step | Correct Method | Common Mistake |
|---|---|---|
| Conversion | Convert 28% to 0.28 | Using the number 28 directly |
| Operation | Divide the part by the decimal (80 / 0.28) | Multiplying the part by the percentage (80 * 0.28) |
| Result | $285.71 (The whole) | $22.40 (The part of the part) |
Always double-check that you are using the correct decimal and performing the right operation for what you are trying to find.
Frequently Asked Questions about Calculating Sums from Percentages
How do I find the total sum if a percentage is known?
To find the total sum, first convert the percentage into a decimal by dividing it by 100. Then, divide the known part by this decimal. For example, if 20% of a sum is $50, you would calculate 50 / 0.20 to get the total sum of $250.
What is the basic formula for percentage problems?
The fundamental formula is Part = (Percentage / 100) * Total. You can rearrange this formula to solve for any of the missing variables. To find the Total, the formula becomes Total = Part / (Percentage / 100).
Can I use this calculation for discounts and tips?
Yes, this method is perfect for those situations. If you know the dollar amount of a discount and its percentage, you can find the original price. Similarly, if you know the tip amount and the percentage you want to give, you can determine the total bill.
Why is it important to convert the percentage to a decimal?
Converting the percentage to a decimal is crucial because it allows you to use it in standard mathematical equations. A percentage represents a ratio out of 100, and the decimal form (e.g., 0.28) is the actual numerical value you need for multiplication and division.
How can I double-check my math on percentage problems?
The best way to check your answer is to reverse the calculation. Once you have found the total sum, multiply it by the original percentage (in decimal form). If the result is the “part” you started with, your calculation is correct.

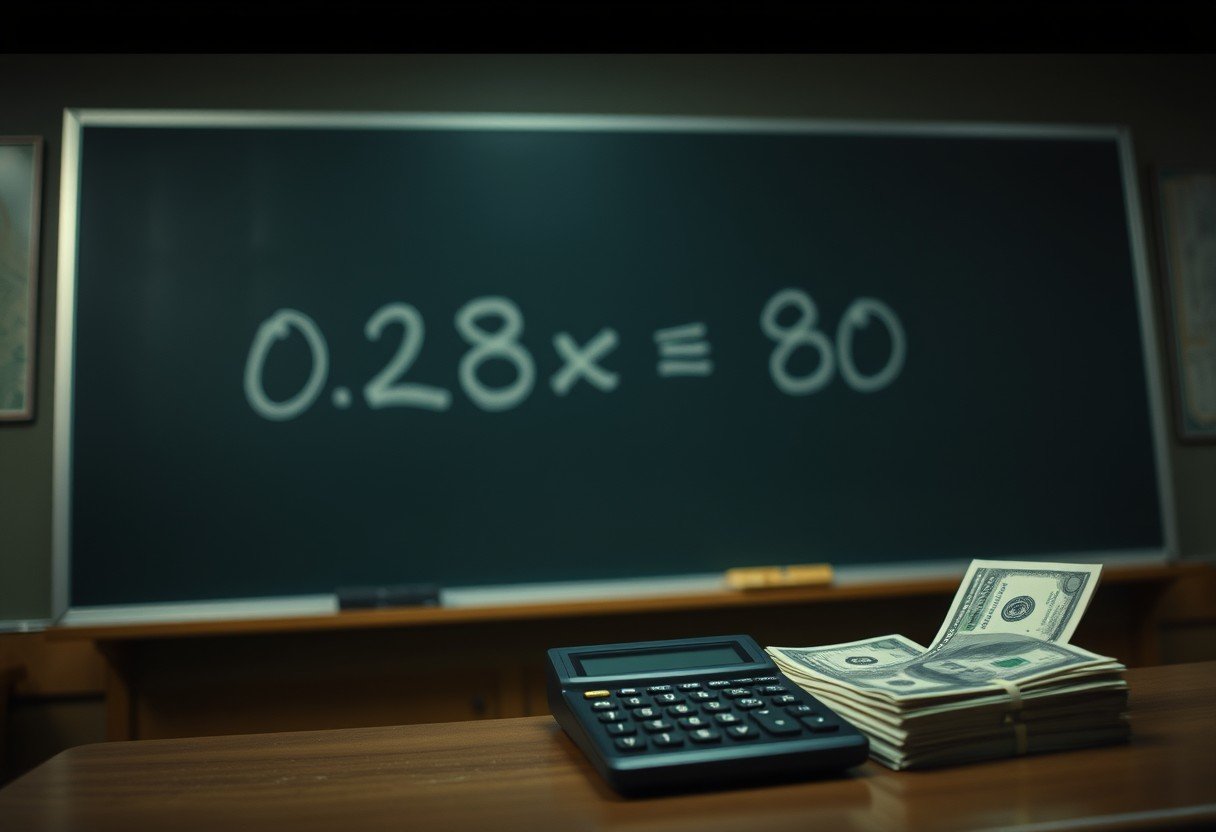







Leave a Comment