With a simple equation like 1 – x = x, you may wonder what value can replace x to satisfy the statement. Understanding how to solve for x in this equation not only boosts your mathematical skills but also enhances your problem-solving abilities. In this blog post, you’ll learn the steps to isolate x, discover its value, and appreciate the significance of balance in mathematical equations. By the end, you’ll have a clear understanding of what one number can replace x in this equation.
Key Takeaways:
- Equation Understanding: The equation ‘1 – x = x’ provides a fundamental algebraic expression that can be solved to find the value of x.
- Solving for X: By rearranging the equation, we find that x can be expressed as x = 0.5.
- Graphical Interpretation: The equation can be represented graphically, illustrating the point where the line for y = 1 – x intersects with y = x.
- Applications: This type of equation has practical applications in various fields, including economics and physics, where balance or equilibrium is analyzed.
- Understanding Variables: The concept emphasizes the importance of understanding how to manipulate and solve for variables in algebraic equations.
Understanding the Equation
For anyone delving into algebra, grasping the fundamentals behind the equation 1 – x = x is crucial. This equation illustrates the relationship between variables and constants, prompting you to find a specific value for x that satisfies the equation. Understanding how to manipulate this equation will enhance your problem-solving skills and allow you to engage with more complex mathematical concepts.
The Basics of Variables
With any equation, variables play a pivotal role as placeholders for unknown values. In the case of your equation, ‘x’ represents an unknown number that must be determined. By solving for ‘x,’ you gain insight into how numbers interact within the equation, laying the foundation for more advanced mathematical pursuits.
The Properties of Equality
The properties of equality are important when working with equations like 1 – x = x. These properties, including the addition, subtraction, multiplication, and division properties, allow you to manipulate both sides of the equation while maintaining balance. This means that whatever operation you perform on one side, you must also apply to the other side, ensuring that the equation remains true.
Variables interact with the properties of equality to enable you to solve equations effectively. By applying these properties, you can isolate the variable, making it easier to find its value. Understanding these concepts will not just aid you with this particular equation, but also equip you with tools for tackling a broader range of mathematical challenges.
Isolating X
If you want to solve the equation 1 – x = x, you need to isolate the variable x. This involves rearranging the equation so that x is on one side, allowing you to determine its value more easily. In doing so, you’ll gain a clearer understanding of how x interacts within the equation, leading you to the solution.
Rearranging the Equation
To isolate x, you should first add x to both sides of the equation. This way, you eliminate it from one side, creating a more manageable equation. Your goal is to consolidate all x terms on one side and constants on the other, enabling a straightforward solution in the next step.
Solving for X
To find the value of x, you’ll now have a simplified equation that allows you to easily perform operations to solve for this variable. By continuing to simplify and isolate x, you will ultimately reveal its true value in relation to the constants on the opposite side of the equation.
The key to successfully solving for x lies in your ability to manipulate the equation step by step. Once you have rearranged the equation to 1 = 2x, you can divide both sides by 2. This will give you the direct value of x. Understanding these steps empowers you to tackle similar equations with confidence in your mathematical skills.
Analyzing Solutions
Despite initial appearances, the equation 1 – x = x holds significant implications for the value of x. By diving deeper into its structure, you can uncover the variable’s potential and understand how it interacts within the equation. The approach you take in analyzing these solutions will be crucial in revealing the essence of the inquiry. Let’s explore further!
Possible Values for X
One of the possible values for x in the equation 1 – x = x is 0.5. When you substitute x with this value, both sides of the equation become equal, confirming its validity. However, it’s important to note that this scenario exists solely within this specific context.
Unique Solutions vs. Infinite Solutions
Solutions can be categorized into unique and infinite types. In this particular equation, you will find that there is a unique solution where x equals 0.5. Unlike some equations that produce multiple valid answers, the singular nature of this equation emphasizes the precise relationship between the terms involved.
The presence of a unique solution in the equation 1 – x = x highlights the clarity of the relationship established through algebra. You can further investigate different equations and scenarios to see how unique solutions compare to infinite ones, where a whole set of values may satisfy the same equation. Understanding these distinctions helps you appreciate the versatility and depth of mathematical concepts.
Practical Applications
Unlike abstract mathematical principles, the equation 1 – x = x has practical applications that resonate in everyday decision-making and problem-solving. For instance, understanding this equation can help you in budget planning, where allocating a fixed amount against variable expenses is crucial. Whether you’re in finance or managing personal accounts, this concept illuminates how balancing equations can simplify complex scenarios and lead to better financial decisions.
Real-World Examples of Similar Equations
Any basic equation you encounter can illustrate similar principles, such as balancing budgets, calculating distances, or even understanding rates of change in various contexts. For example, the common equation for calculating profit, revenue minus costs, mirrors the structure you see with 1 – x = x, reinforcing the importance of balance and clarity in financial contexts.
Implications in Different Fields
Examples of practical implications extend beyond finance into fields such as engineering, physics, and economics. The equation can model phenomena where two opposing forces or changes need to be equal, allowing you to derive solutions that impact design, resource allocation, or predictive analysis.
A deeper understanding of how 1 – x = x applies across various fields can significantly enhance your analytical skills. In engineering, for example, maintaining equilibrium in structural designs relies on similar mathematical principles. In physics, motion equations often require balancing forces, and in economics, understanding market equilibrium allows for more accurate forecasts. Thus, grasping this equation not only serves you academically but also enhances your practical skills in tackling real-world challenges.
Common Misconceptions
Once again, you may encounter several misconceptions regarding the equation 1 – x = x. Many assume that the confusion lies solely in the operations involved, but misunderstandings can arise in various areas, such as the interpretation of variables and their values. By addressing these misconceptions, you’ll strengthen your algebraic understanding and become more confident in solving similar equations.
Mistakes in Solving Algebraic Equations
An unfortunate yet common mistake in solving algebraic equations is neglecting to apply opposite operations correctly. You may inadvertently apply operations incorrectly, leading you to an erroneous conclusion. Ensuring you are consistent in your application of addition, subtraction, multiplication, and division is necessary to arriving at the correct solution.
Misunderstanding Equality
An often overlooked aspect of equations is the concept of equality. Many students mistakenly believe that the equals sign merely indicates a “final answer,” rather than a balance of both sides of the equation. This misconception can lead you to make incorrect assumptions about the relationships between numbers and variables.
Equality signifies that both sides of the equation hold the same value, and this understanding is crucial when manipulating algebraic expressions. If you alter one side, you must make the equivalent changes to the other side to maintain balance. Failure to recognize this can result in incorrect transformations and ultimately, wrong answers. Always bear in mind that the equation represents a relationship, not just a final state.
Further Mathematical Concepts
All mathematical equations and principles interconnect in a vast web of knowledge, deepening your understanding of numerical relationships. As you navigate through these concepts, you’ll discover how different areas of mathematics enhance your ability to solve problems and think critically. Understanding these further mathematical concepts provides a strong foundation for more complex theories, allowing you to apply your skills in various real-life scenarios.
Exploring Linear Equations
The concept of linear equations is fundamental in algebra, where you can identify relationships between variables. You’ll learn how to express these relationships as equations, typically in the form of y = mx + b, where m represents the slope and b the y-intercept. By exploring linear equations, you will gain insight into how changes in one variable affect another, empowering you to analyze trends and make predictions.
Related Algebraic Principles
Principles of algebra extend beyond linear equations, influencing various mathematical frameworks. Understanding these principles helps you grasp the broader implications of your calculations and how they relate to different problem-solving scenarios. You will find that core algebraic concepts, such as the distributive property and the law of integer exponents, serve as building blocks for more advanced topics, reinforcing a comprehensive grasp of mathematics.
Exploring related algebraic principles can significantly enhance your mathematical proficiency. Engaging with concepts like factoring, the quadratic formula, and polynomial identities will sharpen your problem-solving skills and deepen your conceptual understanding. These principles allow you to tackle a variety of challenges, moving beyond simple equations to more intricate mathematical structures. By dedicating time to learning these principles, you will strengthen your analytical abilities and become more adept at mathematical reasoning.
Conclusion
Drawing together the equation 1 – x = x, you find that the solution reveals a specific value for x. By rearranging the equation, you can easily solve for x and discover that x equals 0.5. This reveals how simple algebra can effectively provide answers. Whether you’re solving equations for academic purposes or practical applications in daily life, understanding these concepts enhances your mathematical skills and confidence.
FAQ
Q: What is the equation ‘1 – x = x’ asking?
A: The equation ‘1 – x = x’ is asking to find the value of ‘x’ that makes both sides of the equation equal. It represents a simple algebraic problem where we need to solve for the variable ‘x’.
Q: How can I solve the equation ‘1 – x = x’?
A: To solve the equation ‘1 – x = x’, you can rearrange it as follows: Add ‘x’ to both sides to get ‘1 = 2x’. Then, divide both sides by 2, yielding ‘x = 1/2’.
Q: What does the solution x = 1/2 represent in the context of the equation?
A: The solution x = 1/2 means that if you substitute 1/2 for ‘x’ in the original equation ‘1 – x = x’, both sides will equal each other. Specifically, ‘1 – 1/2 = 1/2’ confirms that the equation holds true.
Q: Are there other methods to check if x = 1/2 is the correct solution?
A: Yes, you can check the solution by plugging x = 1/2 back into the original equation. Substitute ‘1/2’ for ‘x’: ‘1 – (1/2) = (1/2)’. The left side simplifies to ‘1/2’, which equals the right side, confirming that x = 1/2 is indeed correct.
Q: Can this equation have multiple solutions?
A: No, the equation ‘1 – x = x’ has only one solution, which is x = 1/2. Since it is a linear equation, it can only intersect the line at one point, indicating a single, unique solution for ‘x’.
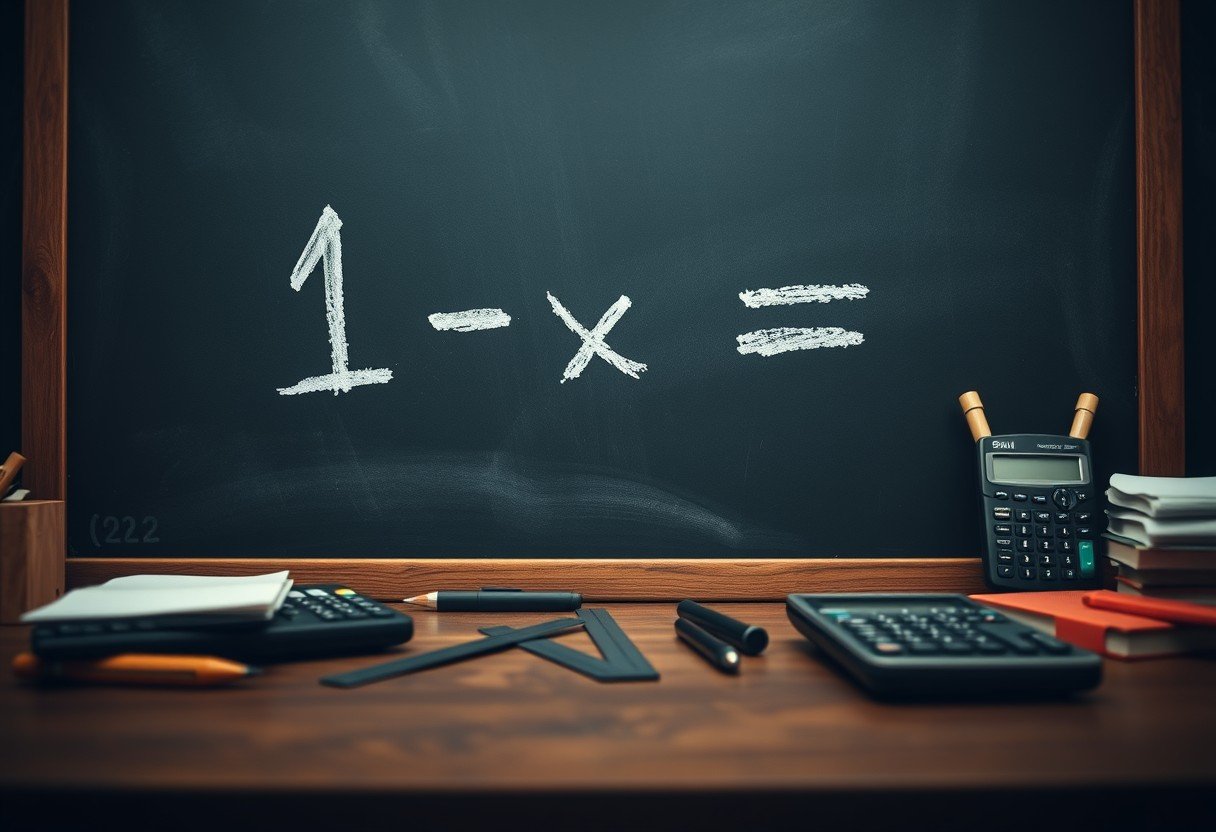
Leave a Comment